【Grasshopper Tutorial】 Plane Pattern

今回は Grasshopper を使用して、上画像の様な、様々なタイプの平面パターンを実装していきます。比較的基本的な 5 種類ピックアップしました。難易度的にはまちまちですが、1 つ 1 つ順を追って進めていけばさほど難易度は高くはありません。初級者向けの記事となっております。

ベース平面作成

最初に上画像 1 枚目の様な、曲面を 5 つ作成していきます。今回は、こちらの 5 つの平面にそれぞれのパターンを描いていきます。

1. 「Construct Point コンポーネント」を使用し、原点(0,0,0)に点を作成します。
2. 「Move コンポーネント」を使用し、作成した点を複製していきます。
3. 「Serise コンポーネント」で入力端子 S・N に 2100、入力端子 C に 5 を入力します。「2100・4200・6300・8400・10500」のリストが作成されます。
4. 「Unit X コンポーネント」で「Serise コンポーネント」で作成したリストを X 方向のベクトル化し、「Move コンポーネント」の入力端子 T に接続します。最初に原点に作成した点が（2100,0,0）…（10500,0,0）の位置に複製されました。「Move コンポーネント」出力端子 G を「Graft」します。
5. 複製した 5 つの点を Z 方向に複製していきます。新たに「Move コンポーネント」を用意し、先ほどの「Move コンポーネント」の出力端子を接続します。
6. 「Serise コンポーネント」を使用し、移動距離のリストを作成します。入力端子 S は 0，N は 300，C は 20 を入力します。
7. 「UnitZ コンポーネント」に「Serise コンポーネント」の出力端子を接続します。
8. 「Move コンポーネント」に「UnitZ コンポーネント」を出力端子を接続します。

1. 上画像の様に Z 方向に点が複製されたものが 5 列できていれば OK です。これらの点を Sin 波を使用してウェーブ状に移動させていきます。

1. 「Remap Numbers コンポーネント」を使用し、「Serise コンポーネント」で作成した Z 方向への移動距離のリストを角度のリストにリマップします。入力端子 V に「Serise コンポーネント」の出力端子を接続します。
2. 「Remap Numbers コンポーネント」の入力端子 S に「Bounds コンポーネント」を使用して作成した、「Serise コンポーネント」のリストの最小値から最大値までのドメインを接続します。
3. 「Remap Numbers コンポーネント」の入力端子 T に「Construct Domain コンポーネント」で作成した、「0 ～ 2π」のドメインを接続します。
4. 「Remap Numbers コンポーネント」の出力端子 R から「0 ～ 2π」までを 20 分割したリストが出力されます。「Sine コンポーネント」にこのリストを接続します。
5. 「Unit Y コンポーネント」に「Sine コンポーネント」を接続し、Sin 波を取得します。
6. 「Multiplication コンポーネント」を使用し先ほど取得した Sin 波に振幅を掛けていきます。今回は 400 を掛けています。
7. 「Move コンポーネント」を使用し、入力端子 G に Z 方向に複製した点を入力し、入力端子 T に「Multiplication コンポーネント」で取得した Sin 波に振幅を掛けたものを接続します。

1. 上画像の様に、点が Sin 波を描いていれば OK です。
2. 「Interpolate コンポーネント」を使用し、作成した点をつなぐ曲線を作成していきます。
3. 「Extrude コンポーネント」を使用し、作成した曲線を X 方向に押し出します。入力端子 B に「Interpolate コンポーネント」で作成した曲線を、入力端子 D に「Unit X コンポーネント」に押し出し距離 2000 を接続したものをつなげます。

1. 上画像の様に曲面が作成されていれば OK です。「Extrude コンポーネント」の出力端子を「Simplify」「Flatten」しときます。
2. コンポーネントをすべてドラッグして選択し、右クリックを押し「Cluster」しておくことでパッケージ化しておきます。これでベースとなる曲面は完成です。

Triangle Mesh

最初に三角形メッシュに分割した平面を作成してみます。今回は「Weaverbird」というプラグインを使用します。

1. 「List Item コンポーネント」で先ほど作成した 5 つの曲面から 0 番目を取り出します。
2. 「Mesh コンポーネント」に接続し、メッシュに分割します。
3. 「Weaverbird’s Split Triangles Subdivision コンポーネント」を使用し作成したメッシュを三角形に分割します。入力端子 L にはメッシュの細かさを入力します。今回は Level2 を入力しています。
4. 「Weaverbird's Picture Frame コンポ―ネント」を使用し、先ほど作成した三角形の各メッシュに穴をあけて完成です。

Voronoi

続いて Voronoi パターンを実装していきます。

1. 「List Item コンポーネント」を使用し、5 つの曲面のうち 1 番目を取り出します。
2. 「Deconstruct Brep コンポーネント」を使用し、取得した曲面をフェイス・エッジ・ポイントに分解します。
3. 「List Item コンポーネント」を使用し、「Deconstruct Brep コンポーネント」で分解したエッジのリストから 0 番目の要素、曲面の下部の直線を取得します。
4. 「List Item コンポーネント」を使用し、「Deconstruct Brep コンポーネント」で分解したエッジのリストから 1 番目の要素、曲面の曲線部分を取得します。
5. 取得したエッジのうち曲線を「Length コンポーネント」で曲線の長さを取得します。
6. 「Unit Y」コンポーネントに「Length コンポーネント」で取得した曲線の長さを接続します。
7. 「Extrude コンポーネント」で取得した曲面下部の直線を Y 方向に押し出します。押し出し距離は、「Unit Y コンポーネント」の出力端子を接続します。これで、XY 平面に縦が曲線の長さ、横が平面下部の直線の長方形が作成されます。

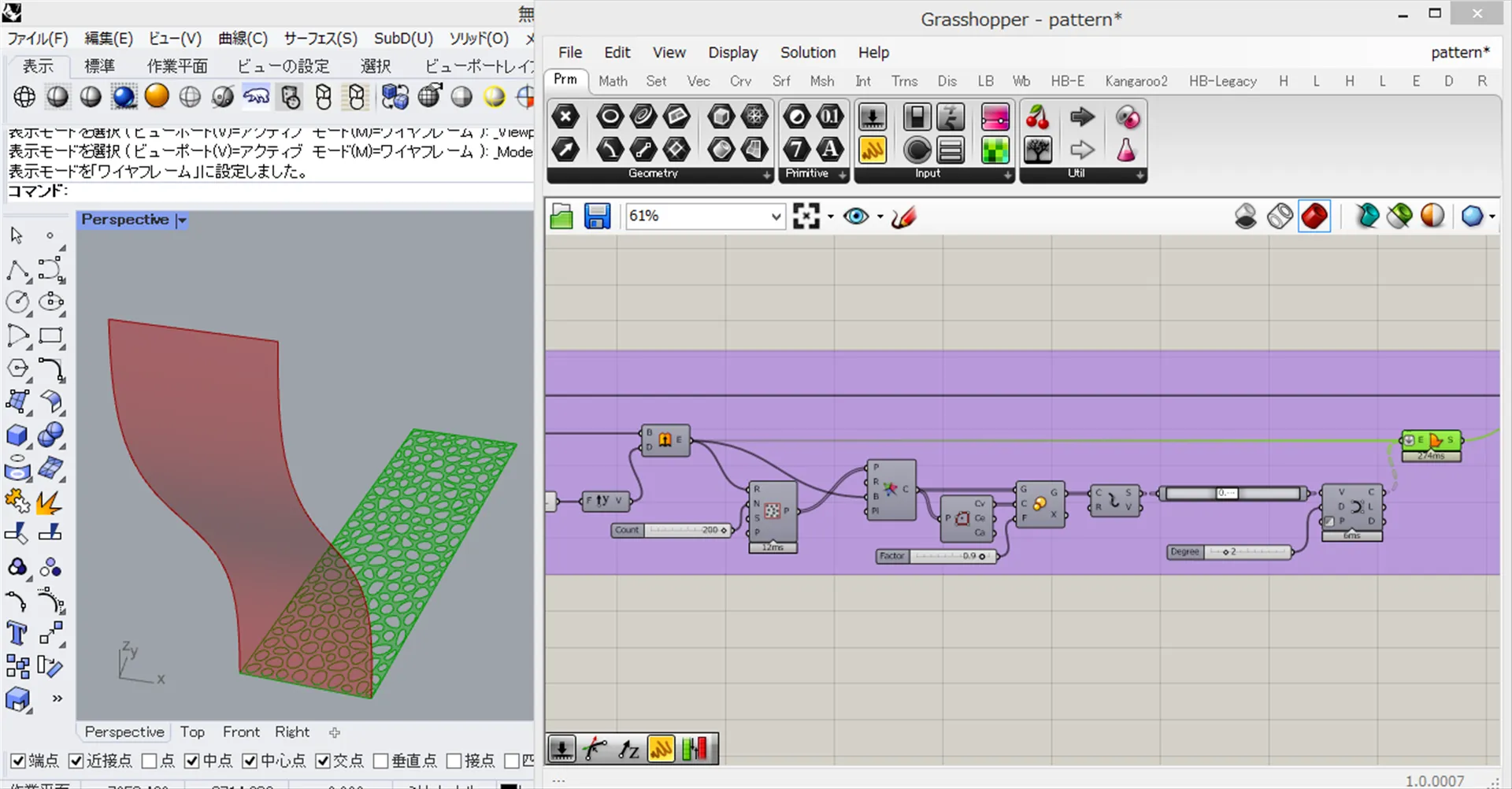
1. XY 平面に作成した長方形を Voronoi 分割していきます。「Populate 2D コンポーネント」を使用し、長方形内にランダムにポイントを作成します。今回は 200 点作成しています。
2. 「Voronoi コンポーネント」を使用し、Voronoi 分割していきます。入力端子 P に「Populate 2D コンポーネント」の出力端子を接続、入力端子 B には「Extrude コンポーネント」で作成した長方形を接続します。
3. 「Polygon Center コンポーネント」を使用し、Voronoi 分割したそれぞれの多角形の中心点を算出します。
4. 「Scale コンポーネント」を使用し、分割した多角形を縮小していきます。入力端子 G には「Voronoi コンポーネント」の出力結果を接続、入力端子 C には「Polygon Center コンポーネント」の出力端子 Cv を接続、入力端子 F には縮小倍率 0.9 を入力します。
5. 「Explode コンポーネント」で縮小した多角形を直線に分解していきます。
6. 「Point on Curve コンポ―ネント」を接続し値を 0.5 とすることで、分解した直線の中点を取得します。
7. 「Nurbs Curve コンポ―ネント」を「Point on Curve コンポ―ネント」の出力端子に接続し、Nurbs 曲線を作成します。入力端子 P は右クリックでメニューを開き「Invert」することで閉じた曲線とします。
8. 「Boundary Surfaces コンポーネント」に「Extrude コンポーネント」の出力端子から得られる、XY 平面に描いた長方形と、「Nurbs Curve コンポ―ネント」の出力端子を接続し、入力端子を「Flatten」することで、上画像の緑部分の様な Voronoi 分割された平面を作成することができました。

1. 長方形に作成した Voronoi 分割を曲面に投影していきます。「Splop コンポーネント」を使用します。入力端子 G に「Boundary Surfaces コンポーネント」で作成した Voronoi 分割した長方形を入力します
2. 「Splop コンポーネント」入力端子 P には長方形の中心点を入力します。「Extrude コンポーネント」に「Area コンポーネント」を接続して取得します。
3. 「Splop コンポーネント」入力端子 S には最初に「List Item コンポーネント」で取得し曲面を入力します。また、入力端子 S は「Reparametrized」しておきます。
4. 「Splop コンポーネント」入力端子 uv には「MD Slider コンポーネント」を接続します。値は(0.5, 0.5)とします。

上画像の様になっていれば OK です。

Circle Plot

次に Circle Plot パターンを実装していきます。

1. 「List Item コンポーネント」を使用し、作成した 5 つの曲面から 2 番目を取得します。
2. 先ほどと同じ手順で XY 平面に縦が曲線の長さ、横が平面下部の直線の長方形を描きます。

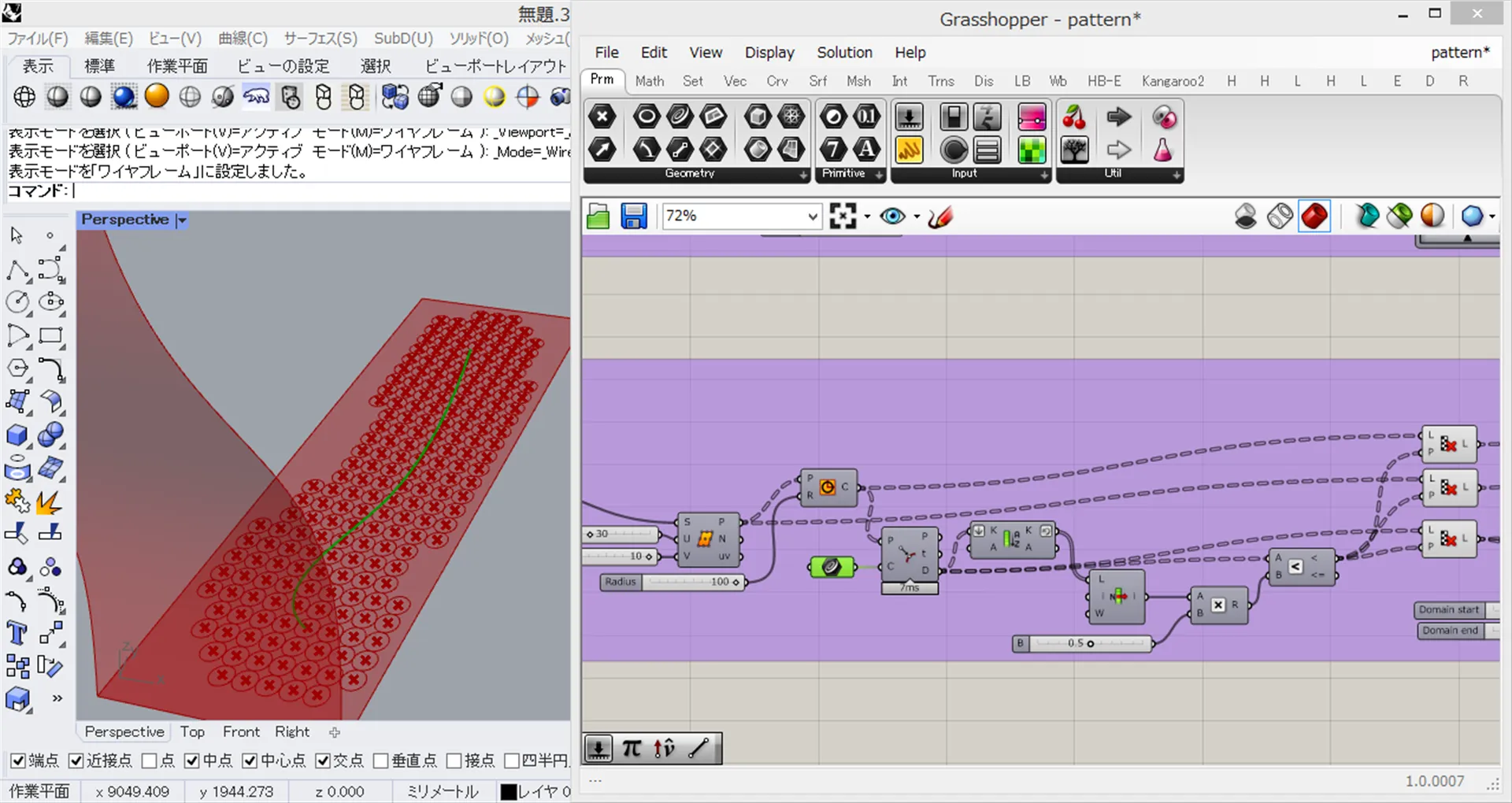
1. 「Divide Surface コンポーネント」を使用し、長方形を指定した個数に分割していきます。今回は縦方向 30, 横方向 10 分割しております。
2. 「Circle コンポーネント」を使用し、各分割点に円を描きます。半径を 100 としてます。
3. Rhinoceros に移動します。長方形内に適当な曲線を描きます。
4. 「Curves コンポーネント」で先ほど描いた曲線をセットします。
5. 「Curve Closest Point コンポーネント」を使用し、分割点に作成した各円の中心から、曲線上の最も近い点を算出します。
6. 「Sort List コンポーネント」を使用し、「Curve Closest Point コンポーネント」で取得した円の中心点から曲線までの最短距離のリストを昇順に並び替えます。入力端子 K で「Flatten」し出力端子 K で「Reverse」します。
7. 「List Item コンポーネント」を使用し、各円の中心から曲線までの最短距離のリストから最も長い距離を取得します。
8. 「Multiplication コンポーネント」を使用し、「List Item コンポーネント」で取得した最長距離を 0.5 倍します。
9. 「Smaller than コンポーネント」を使用し、入力端子 A には「Curve Closest Point コンポーネント」で取得した円の中心点から曲線までの最短距離のリストを接続、入力端子 B には「Multiplication コンポーネント」の出力値を接続し、最長距離を 0.5 倍したものよりも小さいかどうかを Bool 値で取得します。
10. 「Cull Pattern コンポーネント」を３つ用意します。１つ目の入力端子 L には「Circle コンポーネント」の出力端子を接続し、入力端子 P には「Smaller than コンポーネント」で取得した Bool 値のリストを接続します。False の値を間引いていきます。
11. 「Cull Pattern コンポーネント」の２つめ入力端子 L には「Divide Surface コンポーネント」の出力端子 P を接続し、入力端子 P には「Smaller than コンポーネント」で取得した Bool 値のリストを接続します。
12. 「Cull Pattern コンポーネント」の 3 つめ入力端子 L には「Curve Closest Point コンポーネント」の出力端子 D を入力し、入力端子 P には「Smaller than コンポーネント」で取得した Bool 値のリストを接続します。
13. 上画像の様に、曲線付近の円のみが残れば OK です。

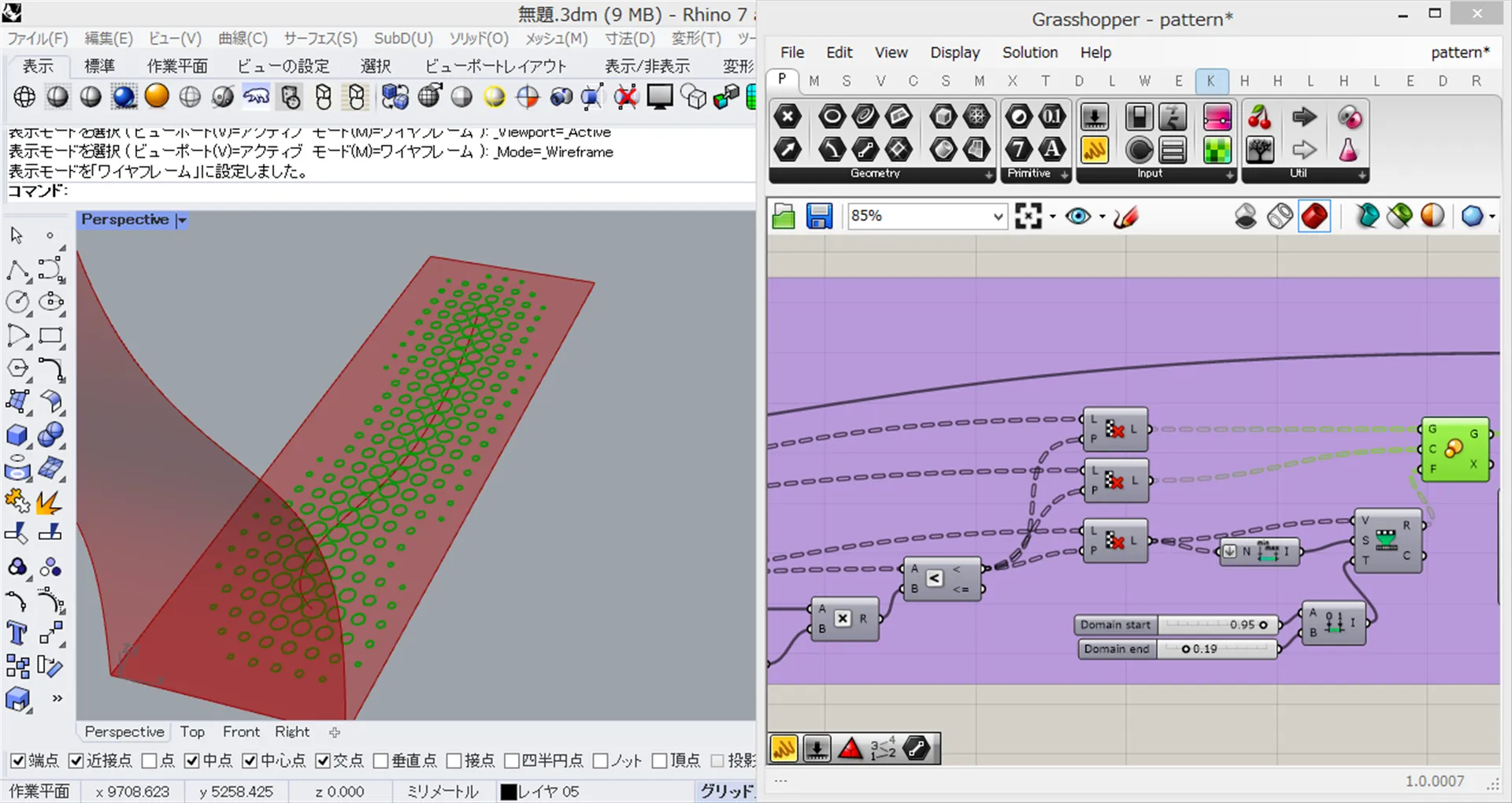
1. 取得した曲線付近の円を曲線からの距離に応じて縮小していきます。「Scale コンポーネント」を用意し、入力端子 G には１つめの「Cull Pattern コンポーネント」で取得した、円を接続します。
2. 「Scale コンポーネント」の入力端子 C には 2 つ目の「Cull Pattern コンポーネント」で取得した円の中心点を接続します。
3. 「Remap Numbers コンポーネント」を使用し、入力端子 V に 3 つ目の「Cull Pattern コンポーネント」で取得した曲線から円の中心点までの距離のリストを接続します。
4. 「Remap Numbers コンポーネント」の入力端子 S に、「Bounds コンポーネント」で取得した「Cull Pattern コンポーネント」のリストの最小値から最大値までのドメインを入力します。「Bounds コンポーネント」の入力端子は「Flatten」します。
5. 「Remap Numbers コンポーネント」の入力端子 T に縮小倍率を入力します。今回は「0.95 ～ 0.19 倍」にしてます。
6. 「Remap Numbers コンポーネント」の出力端子 R から、円の縮小倍率のリストが取得できましたので、「Scale コンポーネント」に接続します。
7. 上画像の様に、曲線から遠くなれば遠くなるほど円が小さくなっていれば OK です。

1. 「Boundary Surfaces コンポーネント」に「Extrude コンポーネント」で取得した長方形と、「Scale コンポーネント」で取得したプロットした円を接続し、境界をサーフェイス化します。入力端子 E は「Flatten」します。
2. 円をプロットした長方形サーフェイスを曲面に投影していきます。「Splop コンポーネント」を使用します。入力端子 G に「Boundary Surfaces コンポーネント」で作成したサーフェイスを入力します。
3. 「Splop コンポーネント」入力端子 P には長方形の中心点を入力します。「Extrude コンポーネント」に「Area コンポーネント」を接続して取得します。
4. 「Splop コンポーネント」入力端子 S には最初に「List Item コンポーネント」で取得した曲面を入力します。また、入力端子 S は「Reparametrized」しておきます。
5. 「Splop コンポーネント」入力端子 uv には「MD Slider コンポーネント」を接続します。値は(0.5, 0.5)とします。

上画像の様になっていれば OK です。

Hexagon

続いて、Hexagon パターンを実装していきます。今回は、Rhino7 で実装されたコンポーネント「TriRemesh コンポーネント」を使用するので、Rhino7 より前のバージョンを使用している方はもしかしたらコンポーネントがないかもしれません。別の方法でも実装できるかと思いますので、チャレンジしてみてください。

1. 5 つの曲面のうち 3 番目を取得します。
2. 今までと同様に、XY 平面に長方形を作成します。

1. 「Extrude コンポーネント」で取得した長方形を「TriRemesh コンポーネント」に接続します。出力端子 T からは、なるべく均等サイズに分割された三角形メッシュが取得できますが、今回は出力端子 D から出力される、三角形の頂点を中心とした六角形メッシュを使用します。
2. 「Face Boundaries コンポーネント」に「TriRemesh コンポーネント」の出力端子 D を接続し、六角形のエッジを取得します。
3. 「Boundary Surfaces コンポーネント」に「Face Boundaries コンポーネント」の出力端子を接続し六角形をサーフェイス化します。

1. 六角形をランダムに間引いていきます。「List Length コンポーネント」に「Boundary Surfaces コンポーネント」を接続し、六角形の個数を取得します。
2. 「Random コンポーネント」を使用し、「0 ～六角形の個数までの数字」をランダムに並べたリストを作成します。入力端子 R には「Countruct Domain コンポーネント」で作成した「0 ～六角形の個数までの数字」のドメインを入力、入力端子 N には「List Length コンポーネント」を接続します。
3. 「Random コンポーネント」の出力端子 R から取得されたリストを「Integer コンポーネント」を使用し整数化します。
4. 「Sort List コンポーネント」を使用し降順に並べ替えます。
5. 「Delete Consecutive コンポーネント」を使用し、隣り合う値が同じ値だった場合にダブりの値を消去します。
6. 「List Item コンポーネント」の入力端子 L に「Boundary Surfaces コンポーネント」を接続し、入力端子 i に「Delete Consecutive コンポーネント」でダブりを除いたランダムなリストを入力します。
7. 上画像緑箇所のように六角形がランダムに間引かれていれば OK です。

1. 今まで同様に、長方形に作成した Hexagon パターンを曲面に投影します。

上画像の様になっていれば OK です。

Birds Nest

最後に Bird's Nest パターンを実装していきます。

1. 5 つの曲面から 4 番目を取得します。
2. 今までと同様に XY 平面に長方形を作成します。

1. 「Deconstruct Brep コンポーネント」を使用し、長方形のエッジを取得します。
2. 「List Item コンポーネント」を４つ用意します。それぞれに長方形の各エッジを取得します。
3. 「Divide Curve コンポーネント」を４つ用意し、取得したエッジを分割します。今回は長手方向のエッジは 30 分割、短手方向は 16 分割しています。出力端子 P を「Simplify」しておきます。
4. 「Jitter コンポーネント」を４つ用意し、それぞれ「Divide Curve コンポーネント」の出力端子 P を接続します。Jitter コンポーネントは取得したリストをランダムに並べ替えてくれます。
5. 「Jitter コンポーネント」の 4 つのうち長手方向の直線 1 個と、短手方向の直線 1 個の入力端子 S に seed 値を入力します。今回は 3 を入力してます。

1. 「Merge コンポーネント」を２つ用意します。「Jitter コンポーネント」で並べ替えた分割点のリストのうち、長手方向１つと短手方向１つをマージします。出力端子はそれぞれ「Simplify」しておきます。
2. 「Line コンポーネント」を作成し、入力端子 A・B に「Merge コンポーネント」をそれぞれ接続します。
3. 上画像の緑箇所の様にランダムに並べ替えた点が直線で結ばれていれば OK です。

1. 今までと同様に長方形上に作成した直線を曲面に投影します。
2. 「Curves コンポーネント」を使用し、曲面を分解した「Deconstruct Brep コンポーネント」からエッジをすべて取得します。
3. 「Pipe コンポーネント」を使用し、取得した曲面のエッジと「Splop コンポーネント」で投影したランダムな直線をパイプ化します。

上画像の様になっていれば OK です。

以上になります。基本的な 5 パターンを選んでみました。理解できたら是非立体へ応用してみてください。

【参考文献】

• AppliCraft : https://www.applicraft.com/
• Youtube : チャンネル名：「June Lee」「Voronoi Gradient Pattern Facade Rhino Grasshopper Tutorial」https://www.youtube.com/watch?v=zCFxSLIOECs
• Giulio Piacentio : https://www.giuliopiacentino.com/weaverbird/